2434 - Using a Robot to Print the Lexicographically Smallest String

info

• 문제 보기: 2434 - Using a Robot to Print the Lexicographically Smallest String
• 소요 시간: 52분 36초
• 풀이 언어: java
• 체감 난이도: 3️⃣~4️⃣ (3.3)
• 리뷰 횟수: ✅

풀이 키워드

스포주의

문자열 해시 그리디

풀이 코드

info

• 메모리: 45640 KB
• 시간: 36 ms

class Solution {
    public String robotWithString(String s) {
        // 첫 글자를 미리 t로 init
        final int n = s.length();
        int[] remained = new int[26];
        char[] sArr = s.toCharArray();
        for (char ch : sArr) ++remained[ch-'a'];

        char[] t = new char[n];
        t[0] = sArr[0];
        --remained[sArr[0]-'a'];

        int i = 1;
        int j = 1;
        StringBuilder sb = new StringBuilder();
        while (sb.length() < n) {
            if (j < 1) {
                t[j++] = sArr[i];
                --remained[sArr[i++]-'a'];
            }
            else if (i == n) {
                //System.out.println("i==n: " + t[j-1]);
                sb.append(t[--j]);
            }
            else if (t[j-1] <= sArr[i]) { // 작거나 같음 -> 출력? 보류?
                boolean smallest = true;
                for (int k = t[j-1]-'a'-1; -1 < k; --k) {
                    if (0 < remained[k]) {
                        smallest = false; // 더 작은 값 발견
                        break;
                    }
                }
                //System.out.println("smallest: " + smallest + " " + t[j-1] + " " + sArr[i]);
                if (smallest)
                    sb.append(t[--j]); // 출력: 지금꺼가 최선
                else {
                    t[j++] = sArr[i]; // 보류: 미래에 더 작은 값 존재
                    --remained[sArr[i++]-'a'];
                }
            }
            else {
                t[j++] = sArr[i]; // 보류: 출력 후보 t[j]보다 sArr[i]가 더 작음
                --remained[sArr[i++]-'a'];
            }
        }

        return sb.toString();
    }
}

풀이 해설

문자열 s를 한번 다 스캔하긴 해야 하는데, 각 문자 당 $O(n)$ 처리가 들어가면 $O(n^2)$이 되고, 이건 문자열 길이 상 어렵다.

그렇다고 $O(n)$으로 쉽게 해결날 작업은 아니기에, $O(n\,logn)$의 알고리즘이 정답이겠거니 했다.

• t[j]는 빈공간이며 마지막으로 삽입한 문자는 t[j-1]에 있다. t는 스택처럼 작동한다.
• sArr[i]는 t에 들어갈 차례가 된 문자이다.

하단의 사고 과정으로 풀이했다.

---

흠 s의 앞에꺼를 떼어서 t 꽁무니에 넣고, 출력할땐 t 꽁무니꺼를 빼다 쓴다고?
👇
ok... 출력하려면 일단 s에서 빼서 t로 이동해야 하네
👇
근데 t에 넣으면 넣을수록 먼저 넣었던게 안쪽으로 밀리잖아?
👇
그러니까 t에 넣기 전에 t의 꽁무니랑 t에 넣을거랑 뭐가 더 lex small한지 판단해야겠네. 꽁무니가 더 작으면 먼저 출력해버리자
👇
아 근데 s의 나머지 문자 중에 꽁무니보다 더 small한게 있으면 여기서 출력하는게 손해구나
👇
그럼 출력 전에 현 상황에서 smallest한건지 판단하는 로직을 추가하자
👇
문자열 길이 범위가 꽤 커서 smallest 판단에 매번 순회하긴 좀 그렇고, 해시 카운터를 두는게 좋겠다
👇
만약 s 순회 끝나기도 전에 t를 다 출력해버리면 무조건 하나 떼어서 t에 주고
👇
s 순회 끝났으면 t에 남은거 쭉 출력해야지

---

caution

꽁무니가 더 작지도 크지도 않고, 같으면?

같으면 출력해야 되나 보류(=t에 넣기)해야 되나 고민이 되는데,

보류하는 것으로 로직을 짜면 다음의 반례에서 WA를 받는다.

s = "bczdaz"

결과: "adzzcb"
정답: "adzcbz"

효율적으로 smallest 여부 판별하기

문자열 길이(n)가 최대 $10^5$이므로, s의 $[i+1,\,n)$ 구간을 다 스캔해서

지금 출력할지 말지 고민중인 t[j-1]보다 작은 문자가 있는지 판단하는 것은 TLE이다.

따라서 remained라는 배열에 s를 구성하는 모든 문자를 해싱해서 카운팅하고,

앞으로 처리해야 할 $[i+1,\,n)$ 구간에서의 문자 카운팅 현황을 알 수 있게끔

s의 문자가 t로 보내질때마다 해당 문자 카운터를 1씩 뺀다.

해당 방식으로는 알파벳이 해봤자 26개이니 $O(26)$으로 smallest를 판별할 수 있게 된다.

🧪 TreeMap 사용해보기

처음엔 최소힙이 생각나서 PriorityQueue를 사용하려고 했으나, remove 측면에서 비효율성이 있었다.

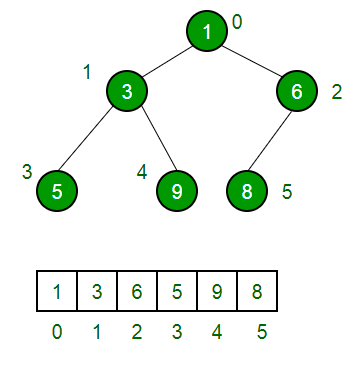
PriorityQueue는 heap 기반 구현으로, 그림처럼 내부적으로 배열에 저장하는데

힙은 BST처럼 좌우간 대소관계 보장을 못하기에 remove가 $O(n)$이다.

이는 dequeue가 $O(log\,n)$이어도 노드 탐색에 선형시간이 걸리기 때문이다.

heap은 상하관계, BST는 좌우관계를 보장하는데

이러한 특징으로 인해 heap은 최소/최대값 구하는데 주로 쓰이고, BST는 이름도 그렇듯이 탐색이 빈번할때 주로 사용된다.

따라서 remained 배열을 컬렉션으로 수정하고 싶다면 PriorityQueue가 아닌 TreeMap을 사용해야 한다.

TreeMap은 RBT로 구현되었기 때문에 balanced BST이며, 자동으로 정렬해준다.

변경 전

for (int k = t[j-1]-'a'-1; -1 < k; --k) {
    if (0 < remained[k]) {
        smallest = false; // 더 작은 값 발견
        break;
    }
}

변경 후

if (remainedMap.lowerKey(t[j-1]) != null) smallest = false;

상단과 같이 smallest 판단에 있어 $O(26)$의 for문 순회를 $O(log\,26)$의 lowerKey로 개선해볼 수 있다.

하단은 전체 코드이며 수행시간은 233ms이다. (변경된 부분은 표시해놓음!)

TreeMap 버전

import java.util.*;

class Solution {
    public String robotWithString(String s) {
        // 첫 글자를 미리 t로 init
        final int n = s.length();

        // ✅ TreeMap 변경: remained 배열 대신 TreeMap 사용
        TreeMap<Character, Integer> remainedMap = new TreeMap<>(); // ✅ TreeMap 변경
        char[] sArr = s.toCharArray();
        for (char ch : sArr) remainedMap.merge(ch, 1, Integer::sum); // ✅ TreeMap 변경

        char[] t = new char[n];
        t[0] = sArr[0];
        remainedMap.merge(sArr[0], -1, Integer::sum); // ✅ TreeMap 변경
        if (remainedMap.get(sArr[0]) == 0) remainedMap.remove(sArr[0]);

        int i = 1;
        int j = 1;
        StringBuilder sb = new StringBuilder();
        while (sb.length() < n) {
            if (j < 1) {
                t[j++] = sArr[i];
                // ✅ TreeMap 변경
                remainedMap.merge(sArr[i], -1, Integer::sum);
                if (remainedMap.get(sArr[i]) == 0) remainedMap.remove(sArr[i]);
                ++i;
            }
            else if (i == n) {
                //System.out.println("i==n: " + t[j-1]);
                sb.append(t[--j]);
            }
            else if (t[j-1] <= sArr[i]) { // 작거나 같음 -> 출력? 보류?
                boolean smallest = true;
                if (remainedMap.lowerKey(t[j-1]) != null) smallest = false; // ✅ TreeMap 변경

                //System.out.println("smallest: " + smallest + " " + t[j-1] + " " + sArr[i]);
                if (smallest)
                    sb.append(t[--j]); // 출력: 지금꺼가 최선
                else {
                    t[j++] = sArr[i]; // 보류: 미래에 더 작은 값 존재
                    // ✅ TreeMap 변경
                    remainedMap.merge(sArr[i], -1, Integer::sum);
                    if (remainedMap.get(sArr[i]) == 0) remainedMap.remove(sArr[i]);
                    ++i;
                }
            }
            else {
                t[j++] = sArr[i]; // 보류: 출력 후보 t[j]보다 sArr[i]가 더 작음
                // ✅ TreeMap 변경
                remainedMap.merge(sArr[i], -1, Integer::sum);
                if (remainedMap.get(sArr[i]) == 0) remainedMap.remove(sArr[i]);
                ++i;
            }
        }

        return sb.toString();
    }
}

메모

• 복습 추천추천 👍
• 실전에서 IOOB 실수를 최소화하려면 t를 Deque으로 구현하는 것이 좋지 않을까