본문으로 건너뛰기

3439 - Reschedule Meetings for Maximum Free Time I

info

풀이 키워드​

스포주의

그리디 슬라이딩 윈도우


풀이 코드​

info
  • 메모리: 60960 KB
  • 시간: 1 ms
class Solution {
    public int maxFreeTime(int eventTime, int k, int[] startTime, int[] endTime) {
        int n = startTime.length; // number of events
        int[] gap = new int[n+1]; // n+1 gaps exist for n events

        // calc gaps
        gap[0] = startTime[0];
        gap[n] = eventTime - endTime[n-1];
        for (int i = 1; i < n; ++i) {
            gap[i] = startTime[i] - endTime[i-1];
        }

        // select k events -> k+1 gaps available
        int sdx = 0, edx = k;
        int sum = 0;
        for (int i = 0; i < k+1; ++i) {
            sum += gap[i]; // init sum
        }

        // sliding window
        int ans = sum;
        while (edx < n) {
            sum -= gap[sdx++];
            sum += gap[++edx];
            ans = ans < sum ? sum : ans;
        }

        return ans;
    }
}

풀이 해설​

eventTime은 최대 10910^9, n은 최대 10510^5라서 무지성 O(n2)O(n^2)은 안된다.

그래서 좀 더 효율적인거 없나 하고 고민해보자면

k개의 미팅을 선택해서 가질 수 있는 최대 영역(이하 가용 영역)에서, 상대 순서를 지킨 채 어떻게 미팅들을 재배치하든

결국 빈 공간의 총합은 같음을 떠올려볼 수 있다.

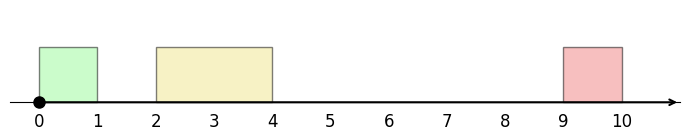
예를 들어 상단과 같은 예제에서는, 3개의 미팅을 선택했을 때

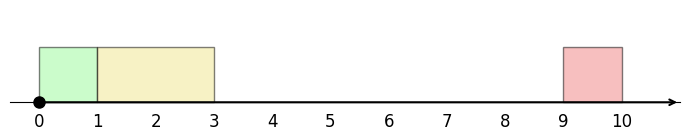
이렇게 배치하든

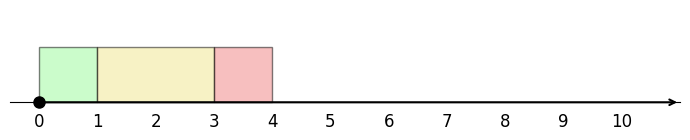
아님 이렇게 딱맞게 배치하든 남은 공간의 총합은 어차피 6으로 동일하다.

그래서 미팅을 직접 재배치하는 시뮬레이션, 완탐, DP 등의 유형은 후보에서 제외된다.


🕊️ 여백의 美​

그렇다면 문제는 가용 영역을 x축 방향으로 옮겨가면서 계산되는 여백의 max 값을 찾는 것으로 풀이된다.

이런 방식의 경우, 진행하면서 도중에 어떤 값을 합산하고 어떤 값을 감산하는지 정해야 한다.

그리고 여기서 약간의 발상이 필요한데, 가용 영역에서 결국 구하고자 하는 것은 여백의 총합이기 때문에

미팅 n개가 있다면 각 미팅 사이사이의 총 n+1개 여백을 대상으로 슬라이딩 윈도우를 적용하는 것과 같다.

(그림은 내일 올림)

int[] gap = new int[n+1]; // n+1 gaps exist for n events

// calc gaps
gap[0] = startTime[0];
gap[n] = eventTime - endTime[n-1];
for (int i = 1; i < n; ++i) {
    gap[i] = startTime[i] - endTime[i-1];
}

따라서 n+1개의 여백들을 gap 배열로 init 하고

// select k events -> k+1 gaps available
int sdx = 0, edx = k;
int sum = 0;
for (int i = 0; i < k+1; ++i) {
    sum += gap[i]; // init sum
}

가용 영역의 총 여백에 대한 윈도우를 init 하고 (k개 미팅 선택시 가용 영역엔 k+1개의 여백 존재)

// sliding window
int ans = sum;
while (edx < n) {
    sum -= gap[sdx++];
    sum += gap[++edx];
    ans = ans < sum ? sum : ans;
}

x축 방향으로 쭉 진행하면서 여백 총합의 max 값을 구하면 T(2n)=O(n)T(2n) = O(n)으로 풀이가 끝난다.


메모​

  • 다소 발상형임. 복습 필요.
  • 예제 생김새에 속지 말고 맨 앞(0)과 맨 뒤(n) gap의 존재를 발상해내는게 관건