본문으로 건너뛰기

440 - K-th Smallest in Lexicographical Order

info

풀이 키워드​

스포주의

수학 트라이


풀이 코드​

info
  • 메모리: 40430 KB
  • 시간: 0 ms
class Solution {
    int n;

    public int calc(long s, long e) { // [s, e)
        int cnt = 0;
        while (s <= n) { // should include n
            cnt += Math.min(n+1, e) - s; // ex. 100 ~ 105 is 106 - 100
            s *= 10; // child prefix
            e *= 10; // child prefix
        }

        return cnt;
    }

    public int findKthNumber(int n, int k) {
        this.n = n;

        int cur = 1;
        k -= 1;

        while (k > 0) {
            // count numbers between two prefixes (ex. 1 ~ 2)
            int cnt = calc(cur, cur+1);

            if (cnt > k) {
                k -= 1; // current
                cur *= 10; // move to child prefix
            }
            else {
                k -= cnt; // skip all children
                cur += 1; // move to sibling prefix
            }
        }

        return cur;
    }
}

풀이 해설​

발상 몰빵형 문제이다. 직접 트라이를 구현해야 하는 것은 아니지만

트라이의 컨셉을 생각해볼 줄 알아야 한다.


트라이와의 유사성​

트라이 구조는 이러한 형태를 지닌다.



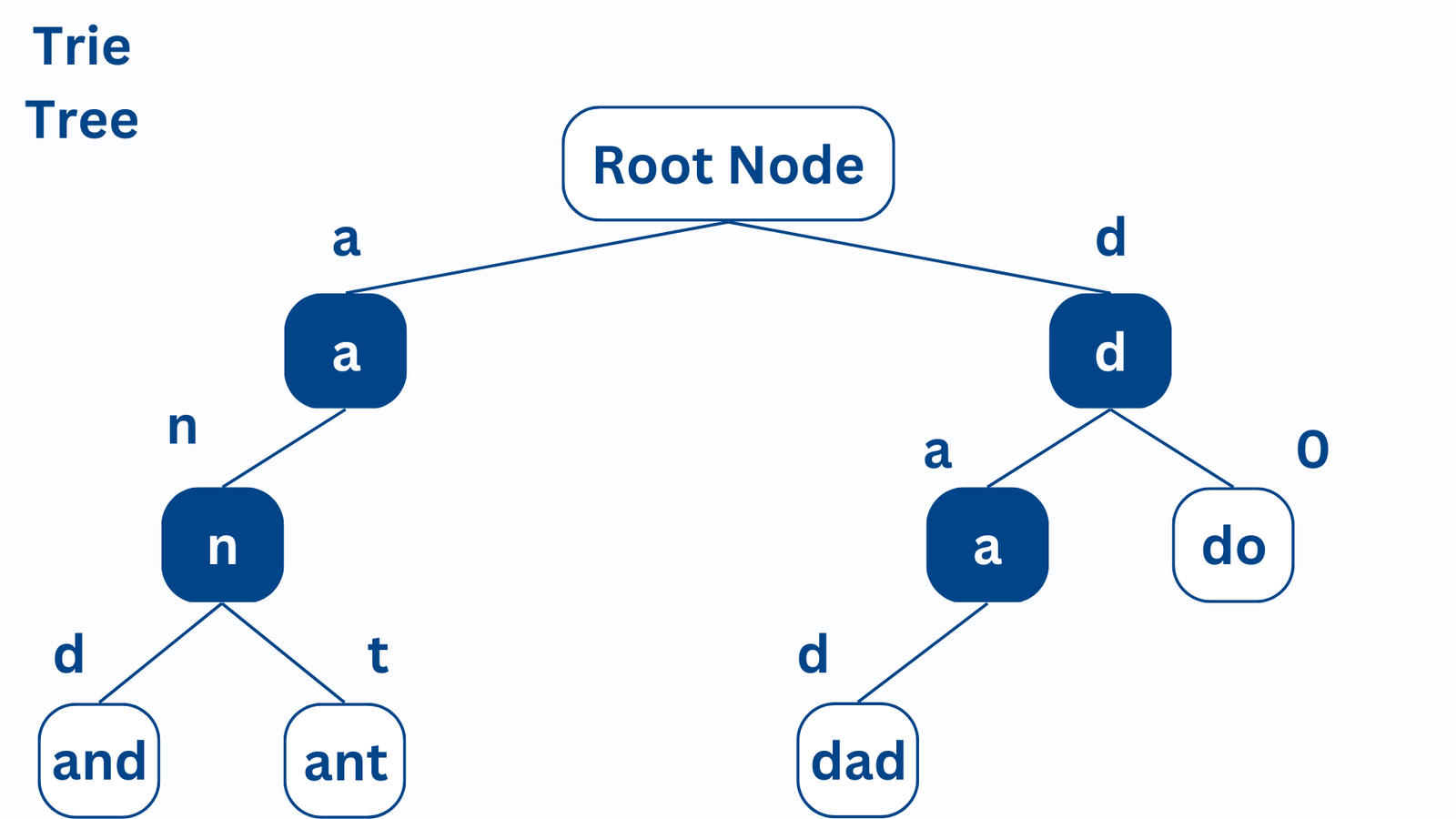
depth가 깊어질수록 문자열의 길이가 늘어나고, sibling 간에는 선후관계가 존재한다.

이 점을 차용하여 lex order로 트리를 구성하면 다음과 같다.

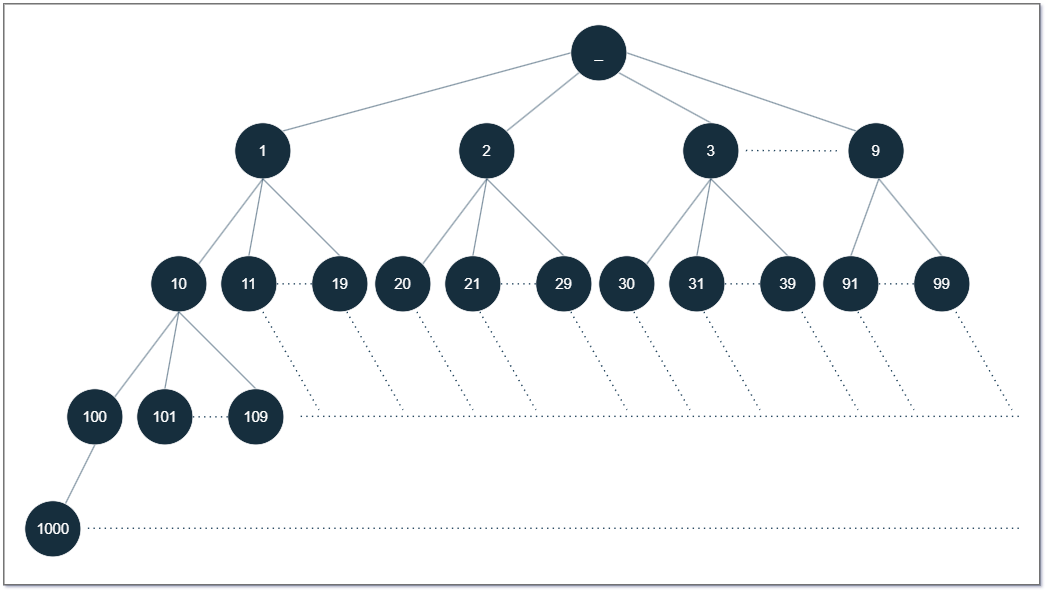
여기서 목표는 k번째 수를 구하는 것인데,

하나하나 노드를 순회하며 세지 않고 서브트리 노드 수를 계산해서 일부 순회를 스킵할 수 있다.

예를들어 n = 11, k = 4 라면 lex order는 [1, 10, 11, 2, 3, 4, 5, 6, 7, 8, 9] 이고 정답은 2인데,

       -
     /...\
    1 ... 9
  / |
10  11

1의 서브트리 노드 수를 구할 수 있다면 굳이 1 하위로는 순회할 필요가 없다는 뜻이다.


서브트리의 노드 수 구하기​

// count numbers between two prefixes (ex. 1 ~ 2)
int cnt = calc(cur, cur+1);
public int calc(long s, long e) { // [s, e)
    int cnt = 0;
    while (s <= n) { // should include n
        cnt += Math.min(n+1, e) - s; // ex. 100 ~ 105 is 106 - 100
        s *= 10; // child prefix
        e *= 10; // child prefix
    }

    return cnt;
}


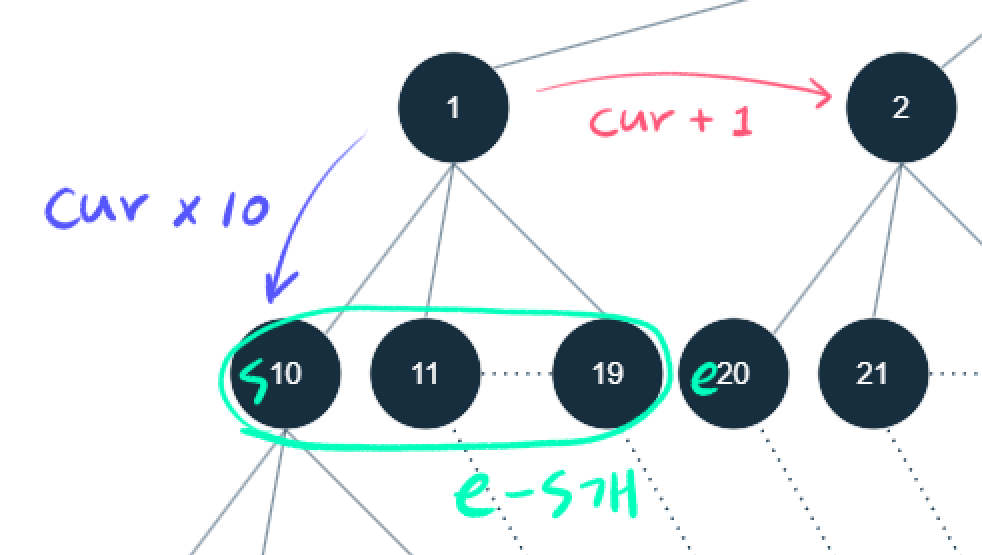
calc는 s가 n을 넘기 전까지 계속 각 레벨의 모든 sibling 개수를 합산한다.

다만 같은 레벨이어도 n을 넘어서 합산하면 안되기에 (ex. n이 11이면 같은 레벨의 12, 13, ... 19를 세면 안됨)

n+1과 e 중 더 작은 값을 limit으로 하여 계산한다.

n이 아닌 n+1인 이유는 노드 n까지 합산해야 하기 때문이다.

calc의 시간복잡도는 레벨 당 상수 시간 연산이 들어가기에 O(log n)O(log\,n)이 된다.


메모​

  • 전체 시간복잡도는 O(log (n)2)O(log\,(n)^2) 이에용